
Much of the support for such programs exists only in lay media (Brzycki, 1995 Hutchins, 2001 Wescott, 1999), with little empirical evidence (Greer, 2005). Training programs have been developed that aim to regulate repetition speed, specifically recommending purposefully slow actions (~10s for the concentric and ~4-10s for eccentric portions). It is unlikely that a single program or method will be effective in realizing all of the possible benefits of resistance training equally. Such outcomes include increased muscular endurance, muscle size, increased muscle strength, increased muscle power, and decreased relative body fat.
Calculation average impulsive force free#
Load, number of sets, number of repetitions per set, number of exercises, mode (machine or free weight), repetition speed, rest period length, exercise order, training frequency, and the specific exercises selected can all be manipulated to promote a precise desired outcome. Several variables can be manipulated in resistance training programs to bring about a specific desired result (Wernbom et al., 2007). What are not simple, however, are the ultimate physiological and morphological effects of resistance training. Because the effect of the earth's gravity is universally present on earth, the physics of resistance training with a constant load (isoinertial) are relatively simple. Performing exercise under any type of resistance is broadly defined as resistance training (Newton, 1999). The data and explanation herein point to superior forces produced by the neuromuscular system via traditional speed training indicating a superior modality for inducing neuromuscular adaptation. However, TUT was greatly increased in the PS condition, with values fourfold greater than maximal acceleration repetitions. Normal speed back squats produced both greater peak and mean propulsive forces than PS action when measured across all loads. An 85kg man performed both normal speed (3 sec eccentric action and maximal acceleration concentric action) and PS back squats over a several loads. A case study of normal versus PS back squats was also performed. While several papers have reviewed the effects of PS, none has yet explained such resistance training in the context of the impulse-momentum relationship. PS is recognized by ~10s concentric and ~4-10s eccentric actions. I would start with 0.1 ms and see what you get.The purpose of this brief review is to explain the mechanical relationship between impulse and momentum when resistance exercise is performed in a purposefully slow manner (PS). You should use a time step that is at least 1/4 of that. Assume a 50 g ball dropped from 1 m high: If we do indeed assume a 1 mm deformation of the little spring, then we can compute the impact time. If this spring deforms no more than 1 mm, it has to be able to store all the energy of the ball (where energy stored $E=\frac12 k x^2$ must be equal to the kinetic energy just before the collision, which is $\frac12 m v^2 = m\cdot g \cdot h$, the potential energy at the top of the trajectory). The collision time depends greatly on the size of the ball and the elastic properties of the ball and the surface - and the force-displacement relationship is not linear but you could simplify things by assuming there is a small (but powerful) spring between ball and ground, with a very high $k$ value. Eventually, the solution will not change (much) when you make the time step shorter - then you will have a short enough step. You could do this by repeating the calculation multiple times, each time reducing the time step by 2x. The force will change during the collision - and given the very simplistic integration method you use, you have to integrate over sufficiently short steps during which the force doesn't change much. For most real world collisions, 0.1 second will be much too long. You need the integration step to be much shorter than the impact time. This way I don't have to use integrals and I ease the calculations, though they won't be accurate but it's hard for a computer to simulate the world literally. In this program I define $dt$ as constant equals to 0.1, then I simply say :

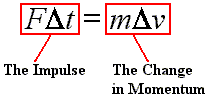
Calculation average impulsive force how to#
So, how to do that ? and why is this force so enormous that it stops the ball almost instantly ? Edit

I have a working collision detection and I know the velocity of the ball before collision, what I want to know is the instantaneous impulse force acting on the ball on collision with the ground. The program didn't work, the ball went through the ground, I'm sure I applied the impulse force and the Normal force together, the force is greater than weight but is still small. I've made a program which is supposed to simulate free fall of a ball on a ground.įor collision with the ground I relied on calculating the impulse force with the answer in this Phys.SE question but I think the law is, well, wrong, the force must be a very big force acting on short time.


 0 kommentar(er)
0 kommentar(er)
